Contents
So far, we’ve covered “scales” and “keys”. Now, let’s talk about an even more fundamental topic before delving into the specifics of melody, chords, and rhythm. That’s the topic of timbre.
We all know that the timbre of a piano is different from that of a guitar, but what exactly makes them different? This is essential knowledge in music production, so I’d like to discuss it before moving on to the next chapters.
1. Sound Spectrum
The most decisive factor in timbre is the component of frequencies. You should know the word “frequency” but what’s the “component”? Let me explain.
Frequencies are associated with pitch, representing the “height” of a tone. When tuning a bass or guitar, you often see frequencies like “xxHz”, which might look light only that specific frequency is present when you play a note. However, it’s not true. In reality, even when playing a single note on an instrument, it contains a wide range of frequencies as components.
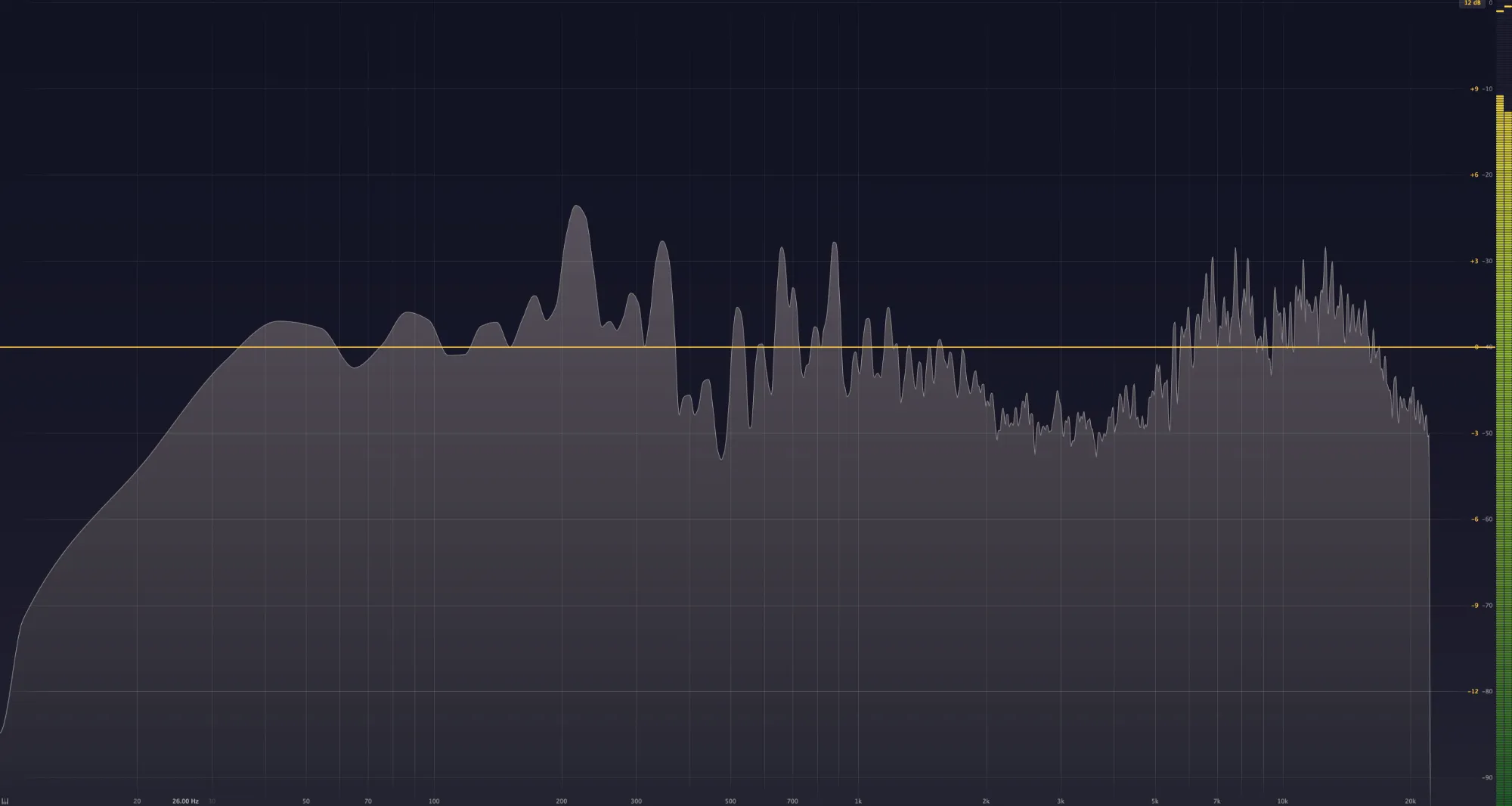
This is an analysis of the frequency components of a single bass note, visualized by a spectrum analyzer.
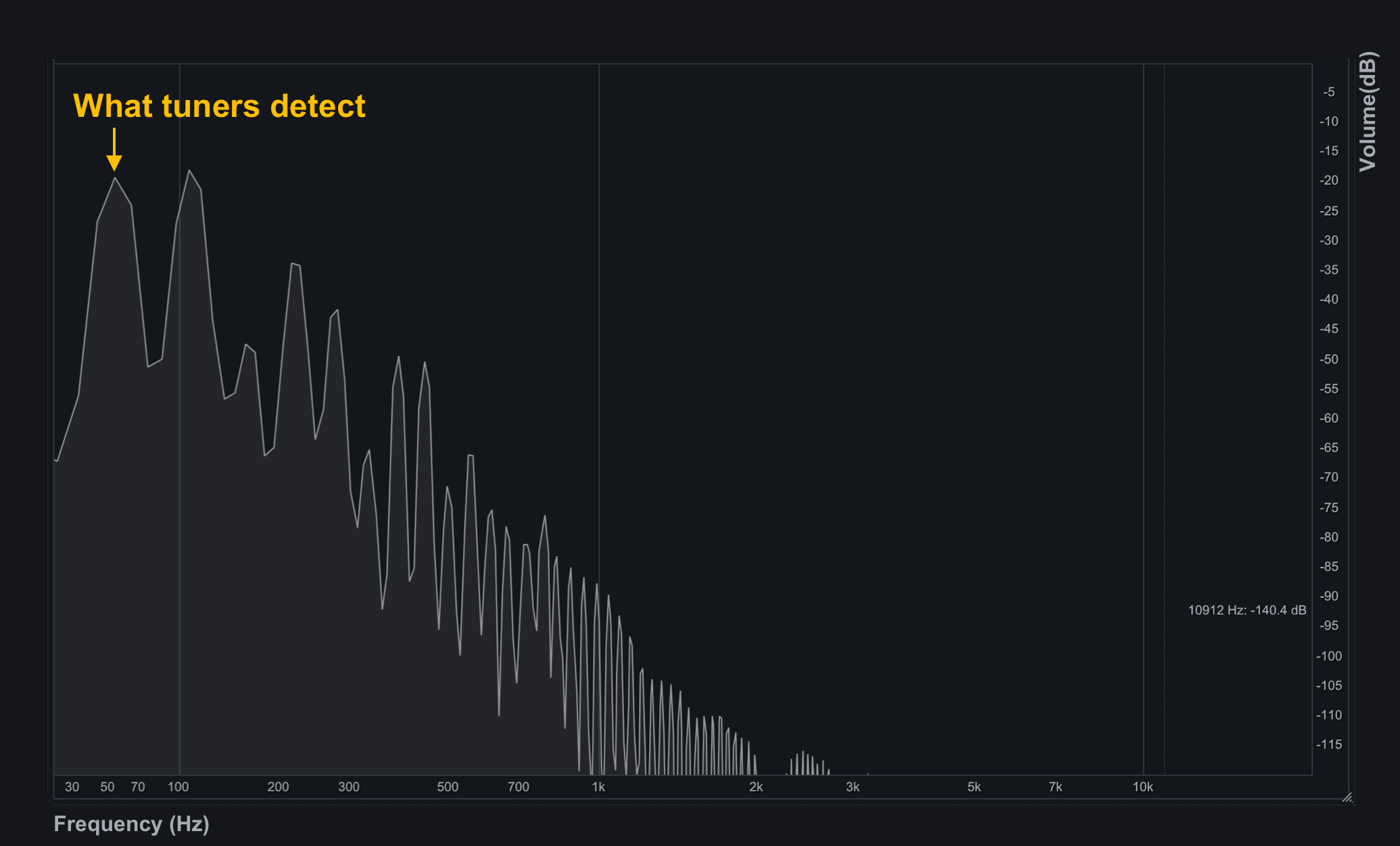
The prominent part is the low frequency below 200Hz, but it’s also generating high-frequency components around 10k(=10,000)Hz. What a tuner detects is the frequency of the most prominent peak, in this case, around 55Hz.
This spectrum concept has similarities with color perception. Just as combining red and green light creates a yellow light, we perceive the result of the synthesed light, not the individual lights. Similarly, in the case of timbre, what we hear as a single tone is actually the result of the synthesis of multiple frequencies.
To put it more frankly, this is similar to the ingredients of food. When you taste ketchup, you primarily detect the taste of tomatoes, but it also contains ingredients like onions or garlics, which contribute to the overall “ketchup flavor”. Similarly, with musical instruments, while you perceive the main frequency as its pitch, you experience the combined frequency components as timbre.
2. Overtones
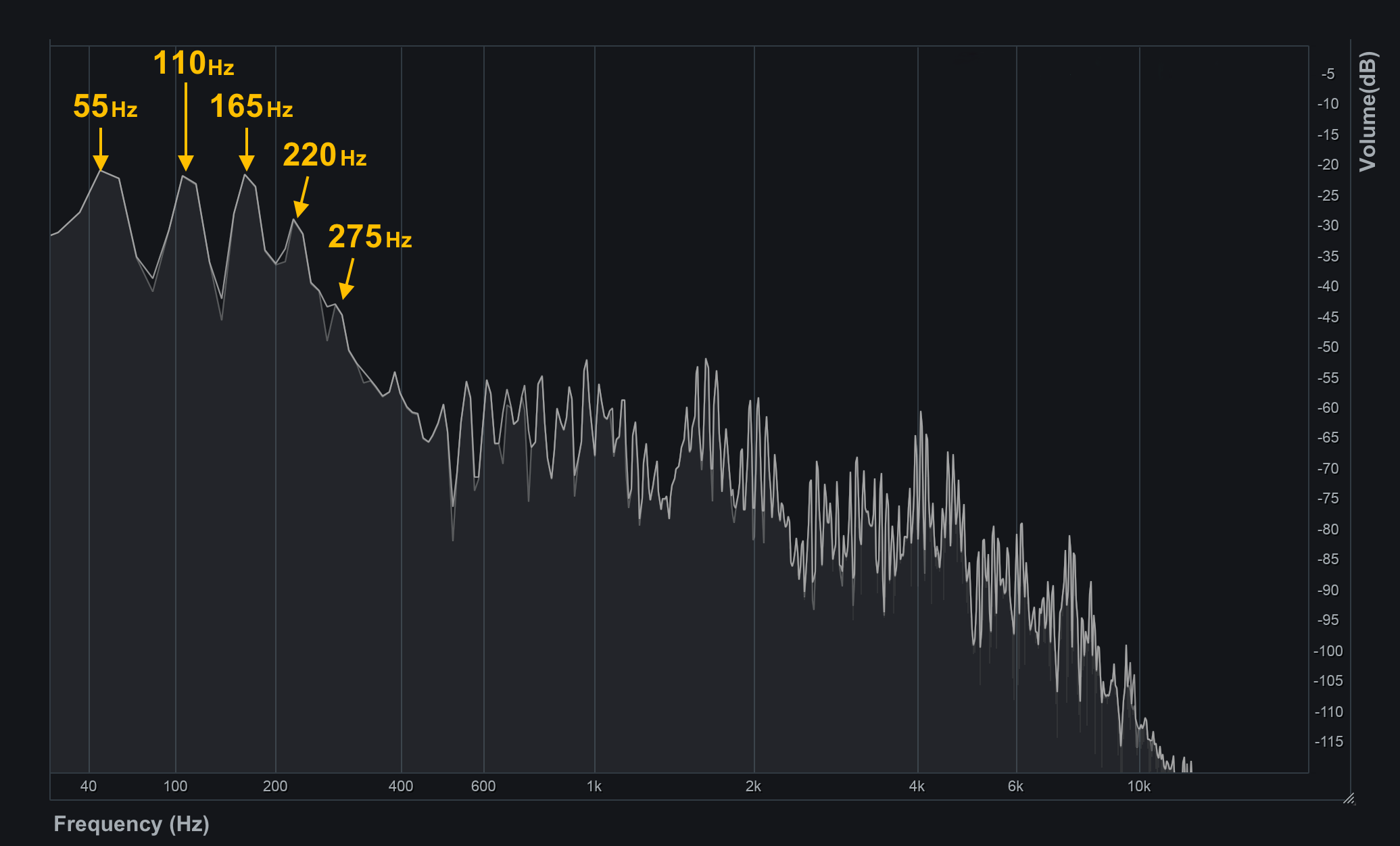
When you analyze one step deeper, you discover something interesting. If you follow the “peaks” of the spectrum, after 55Hz, you find them at 110Hz, then 165Hz and so on.
…Have you noticed the pattern? The frequencies are multiples of the initial peak frequency! This characteristic is common not only to bass guitars but also to any musical instruments such as pianos, guitars, brasses, strings, etc.
The lowest frequency peak is termed the Fundamental and the frequencies that are integer multiples of the fundamental frequency are called Overtones, or Harmonics.
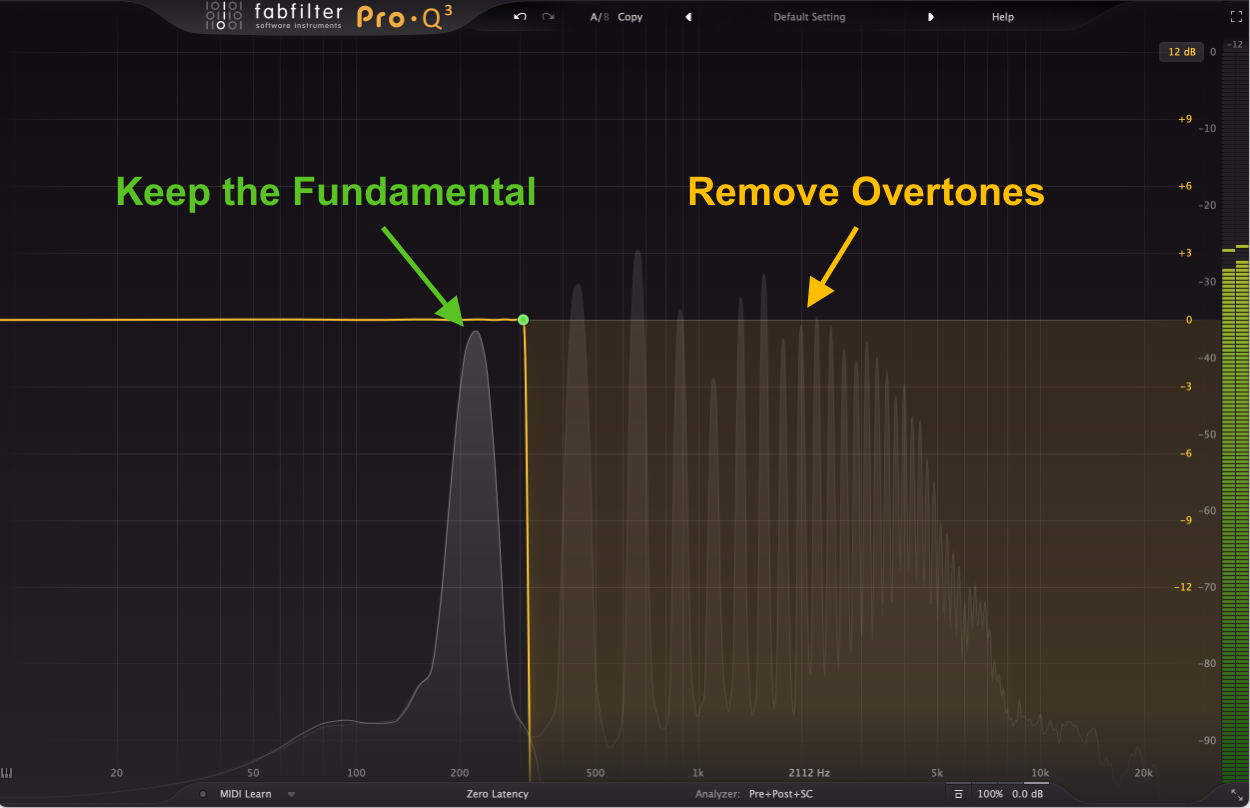
The fundamental determines the pitch that tuners detect. And, all the other components determine (a large part of) timbre. You can easily confirm this by experiments like removing all these overtones by an EQ(equalizer) effect.
The tones above are the instruments that you just heard at the beginning of this article. But surely you cannot distinguish what each sound originally is!
- The original timbres
All the sounds became tasteless. It’s just like separating all ingredients from many kinds of beverages and everything turns into water! This is the big secret about timbre.
Waveforms and Noises
Timbre is associated with spectrum components. And when you record different tones, they show different waveforms. So a waveform, a spectrum, a timbre—These are in a mutually related ‘trinity’ relationship.
The waveforms of acoustic instruments are complex as they come with many elements such as performance noise, temporal changes, and fluctuations. On the other hand, classic synthesizers have very simple basic waveforms so let me take them as examples.
Typical synths offer five basic waveforms like the ones above, and you can switch between them using knobs or whatever. All of them have mathematically simple and unique overtones— Sine waves contain no overtones, triangle and square waves contain only odd-order overtones, and saw waves contain all integer-order overtones. As you can hear, timbres with more harmonics tend to have a brighter or more glaring sound.
Furthermore, white noise is highly distinctive, containing all frequencies, both integer and non-integer, in an almost equal level. When non-integer harmonics increase, the sound becomes noisy, and pitch recognition gradually becomes difficult. The extreme case of this is white noise, which completely lacks pitch perception. In the realm of timbre, you can view it like the purest sine wave and the most random white noise exist at opposite poles, with all other timbres lying in between.
Remember that these components are not in absolute values like “Saw waves have a strong presence at 1000Hz.” Instead, they are in relative ratios to the fundamental Hz. When the relative structures of spectrum are the same, then the waveforms will be the same too, and you recognize them as the same sound.
3. Spectrum and Sound Making
Understanding the spectra of sounds is crucial for sound production and mixing.
For example, in cheap earphones or smartphone speakers, you may not hear much low-frequency area. However, you can mostly recognize the sound of bass instruments, thanks to the presence of overtones. Even if the fundamental is hardly audible, you can still perceive the presence of the instrument due to the higher-frequency components in the spectrum. However, when it comes to the sounds like sub-basses primarily based on sine waves, situations change.
Can you hear the bass sound? As mentioned earlier, sine waves don’t have any overtones, so such sounds may be completely inaudible depending on the environment, posing a risk of significantly altering the impression of the song. To prevent this, various approaches can be taken, such as adding the notes octaves higher, blending different waveforms, or applying distortion to alter the frequency components.
Alternatively, looking from the opposite perspective, you can also focus on the fact that bass instruments often produce high-frequency content. By identifying and reducing what you consider unnecessary parts using an EQ, you can make room for other instruments.
Cutting spectrum with EQAs a music listener, you may have adjusted sounds using an equalizer in a music app, which balances the overall sound of the entire song. However, as a track maker, you will use EQ to adjust the timbre of each individual instrument.
Historical Perspective
Understanding timbre from its mechanism allows you to apply it in various situations. While this may seem a bit physics-oriented, overtones are closely related to harmony theory as well, and therefore are often introduced early in classical music theory books, in fact.
Not having a spectrum analyzer, they use sheet music instead to illustrate the spectrum. While we won’t go into it here, representing the spectrum in sheet music can provide intriguing insights regarding harmony.
The fact that a single note actually contains a variety of pitches is highly intriguing. In Western music theory, theorists have believed for centuries (especially in the 18-19c) that this phenomenon can be used to unravel the secrets of harmony from the logic of physics. In reality, however, such research has its imperfections and is highly questioned in academia today. But some recent books still present the overtone series as a foundation for harmony theory.
Anyway, it is undeniable that the spectrum plays a role in the construction of harmony. In the later chapters, you’ll find several occasions where this knowledge will come in handy. That’s one of the reasons why I introduced this topic in the preparatory section.
Summary
- Timbre is determined by the frequency components of a sound, which can be analyzed using a spectrum analyzer.
- Instrument timbres consist of the fundamental frequency and many overtones that are integer multiples of it.
- Non-integer multiple frequency components create noisy timbres, and when all components are at equal levels, it becomes white noise.
